数表排列规律与位置确定方法

基本规律概述

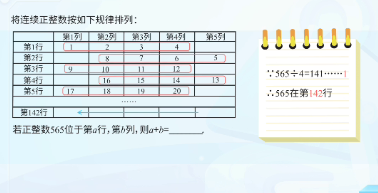
在连续排列的正整数数表中，当每行数字个数相同时，会呈现明显的周期规律。利用这种规律，我们可以高效地确定任意正整数N在数表中的具体位置。

确定步骤：

1. 将N除以每行数字的个数（即周期长度）
2. 通过得到的商和余数确定N所在的行和列
   

   正偶数排列的特殊规则

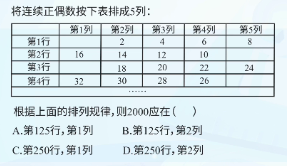
在新题目中，数表由正偶数排列组成，具有以下特点：

• 每行固定四个数字
• 奇数行（第1、3、5...行）数字从左到右依次增大
• 偶数行（第2、4、6...行）数字从右到左依次增大
• 行与行之间首尾数字顺次相接

示例分析：确定2000的位置

1. 计算序号：2000是第1000个偶数（因为2000÷2=1000）
2. 确定行数：将1000除以每行4个数字，得到250，表明2000位于第250行
3. 确定列数：
   • 第250行是偶数行，数字从右向左增大
   • 2000作为该行最后一个数字，位于第一列
   • 因此2000的位置是第250行第1列（选项C）
     

     通用方法扩展

对于正偶数N：

1. 首先计算N÷2得到其在偶数序列中的序号
2. 然后用这个序号除以每行数字个数
3. 根据商确定行数，余数确定列数
4. 注意偶数行和奇数行的排列方向差异

对于正奇数：

可以通过以下方法转换处理：

1. 将奇数加1转换为偶数（N+1）
2. 按照上述偶数处理方法确定位置
3. 必要时再调整回原始奇数的位置

总结

通过分析数表中连续排列的整数（正整数、正偶数或正奇数）的周期规律，我们可以建立一套系统的定位方法。关键在于：

• 理解数表的基本排列规则
• 掌握从数字到序号的转换
• 利用除法运算分解出行列信息
• 注意不同行排列方向的差异
  
  这种方法不仅适用于简单的数学问题，也可以推广到更复杂的数据排列分析中。