39、等比数列
这篇文章教你轻松理解等比数列：一列数字中每个数都是前一个数乘以相同的数（公比Q）。学会用公式求第n项（Aₙ=A₁×Qⁿ⁻¹）和前n项和（Sₙ=A₁×(1-Qⁿ)/(1-Q)）。通过具体例子（首项1，公比2/3）演示如何计算第15项和前20项和，记住三步解题法：找首项、定公比、选公式，多练习就能掌握！
轻松理解等比数列
什么是等比数列？
想象你有一列数字，从第二个数字开始，每个数字都是前一个数字乘以相同的数。这样的数列就叫做等比数列。那个相同的乘数我们叫它公比，用字母Q表示（Q不能为0）。
数列规律公式可以写成：
第n项 = 第1项 × 公比^{(n-1)}
或者用字母表示：
A_n = A_1 × Q^{(n-1)}
小贴士：如果一列数字全都一样（比如3,3,3,...），它既是等差数列（差为0），也是等比数列（公比为1），这种情况我们暂时不重点研究。
怎么求等比数列的和？
如果你想计算前N个数的总和，可以用这个公式：
注意：这个公式在公比≠1时使用
实际例子来啦！
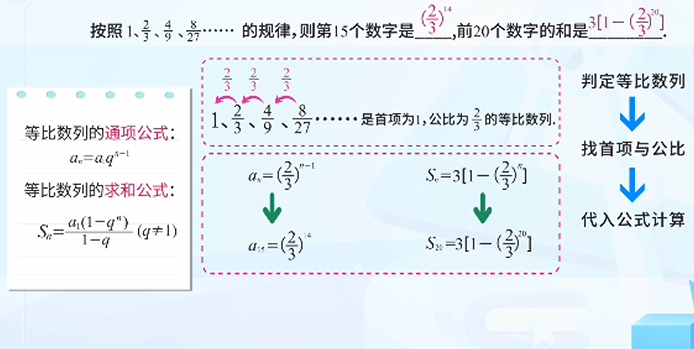
我们来看一个具体的等比数列：
- 第一个数：1
- 公比：2/3（也就是每个数都是前一个数的三分之二）
动手算一算
-
第15个数是多少？
-
前20个数的总和是多少？
解题小窍门
遇到等比数列的题目时，记住这三个步骤：
- 找到第一个数（A₁）
- 确定公比（Q，就是后一个数除以前一个数得到的值）
- 选择合适的公式：
- 求某个位置的数？用第一个公式
- 求总和？用第二个公式
只要掌握这三点，等比数列的题目就变得很简单啦！刚开始可能会觉得有点难，多练习几个例子就会越来越熟练的~
收藏