有理数比较大小：数轴与法则的巧妙运用

同学们好！欢迎来到初中数学营地。今天我们要一起探索有理数比较大小的奥秘。让我们跟随小李的故事，轻松掌握这个重要知识点。

一、数轴上的大小关系

上回讲到，小李和伙伴们把马路看成数轴，将图书馆的位置设为原点，各自家的位置在数轴上表示了出来。现在，他们有了新的疑问：这些数谁大谁小呢？

数学小窍门：在数轴上，有理数从左到右的顺序就是它们从小到大的顺序。也就是说：

• 右边的数总比左边的大
• 左边的数总比右边的小

根据这个规律，我们可以轻松比较几个数的大小关系。例如：
-4 < -3 < 0 < 1 < 3

二、重要发现：正数、负数与零的关系

仔细观察数轴，我们有了第一个重要发现：

1. 正负数的位置关系：
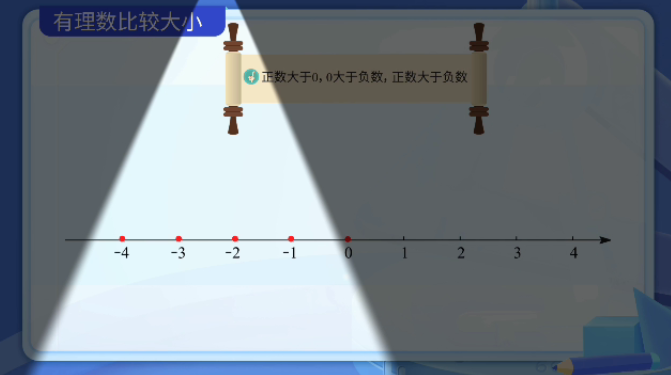
   • 正数都在零的右边
   • 负数都在零的左边
   • 根据"右边的数比左边的大"可以得出：
     • 正数 > 0
     • 0 > 负数
     • 正数总是大于负数

三、负数比较的奥秘

现在我们把目光集中在原点左侧的负数部分。根据数轴规律：
-4 < -3 < -2 < -1

第二个重要发现：

• 对于负数来说，离原点越远的数越小
• 而点与原点的距离正是这个数的绝对值
• 因此得出结论：两个负数比较时，绝对值大的反而小

四、两种比较方法实战演练

方法一：利用数轴比较

例题1：比较-2, 0, 3, -1的大小

解题步骤：

1. 先在数轴上标出这些数的位置
2. 根据"右边的数比左边的大"得出大小关系
3. 最终结果：-2 < -1 < 0 < 3

方法二：利用比较法则

例题2：比较-3/4, -5/6, 1的大小

解题步骤：

1. 先比较正负数：1最大（因为正数>负数）
2. 比较两个负数-3/4和-5/6：
   • 第一步：求绝对值：| -3/4 | = 3/4，| -5/6 | = 5/6
   • 第二步：比较绝对值：3/4 = 9/12，5/6 = 10/12 → 9/12 < 10/12
   • 第三步：根据"绝对值大的负数反而小"，得出-3/4 > -5/6
3. 最终结果：-5/6 < -3/4 < 1

五、总结归纳

今天我们学习了有理数比较大小的两种方法：

1. 数轴法：将数标在数轴上，右边的数总比左边的大
2. 法则法：
   • 正数 > 0 > 负数
   • 两个负数比较：绝对值大的反而小

特别提醒：对于多个负数比较时，可以按照"求绝对值→比较绝对值→反序排列"这三步快速解决。

今天的数学之旅就到这里，希望同学们都能掌握有理数比较大小的技巧。下次课我们再见！