有理数加减法的运算法则详解

一、减法法则：减法转加法的原理

在有理数运算中，减法可以转化为加法来计算，这是非常重要的一个法则。具体来说：

减去一个数，等于加上这个数的相反数
用数学表达式表示就是：a - b = a + (-b)

实际应用示例：
计算 5 - 3 时，可以看作 5 + (-3) = 2
计算 -2 - 4 时，可以看作 -2 + (-4) = -6

这个法则的优点是能够将所有的减法运算统一为加法运算，使计算过程更加规范。

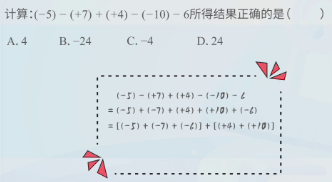
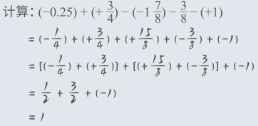
二、有理数加法运算律

有理数的加法运算遵循以下两个基本定律：

1. 加法交换律

两个数相加，交换加数的位置，和不变
公式表示：a + b = b + a

示例：
3 + (-5) = -5 + 3 = -2

2. 加法结合律

三个数相加，先把前两个数相加，或者先把后两个数相加，和不变
公式表示：(a + b) + c = a + (b + c)

示例：
(2 + 3) + (-4) = 2 + [3 + (-4)] = 1

三、运算技巧：正负数分组法

利用加法运算律，我们可以将正数和负数分别分组计算，使运算更简便：

1. 先将所有减法转化为加法
2. 把正数和负数分别组合在一起
3. 分别计算正数之和与负数之和
4. 最后将两个结果相加

小提示：
当计算一个负数加一个正数时，可以看作是用较大的绝对值减去较小的绝对值，然后取绝对值较大的数的符号。