数轴基础知识详解

数轴的基本概念

1. 数轴的定义：竖轴是数轴的一种表示方式，每一个点都代表一个具体的数。原点(0点)是数轴上最重要的参考点，它将数轴分为左右两部分：

   • 原点右侧表示正数
   • 原点左侧表示负数

2. 数轴的作用：

   • 可以直观地表示和比较数值大小
   • 例如：数轴上点A表示2，点B表示-3，两点之间的距离就是5个单位长度
   • 不仅能展示数值位置，还能清晰呈现数值间的相对大小和距离关系

3. 原点的意义：原点是确定其他数值正负和大小关系的基准点，在解决数学问题时起着关键作用。

相反数在数轴上的表示

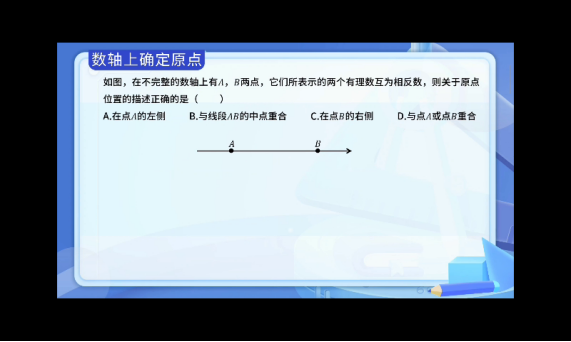
1. 相反数的特点：如果两点表示的有理数互为相反数（如2和-2），那么它们到原点的距离一定相等。

2. 原点位置的确定：

   • 互为相反数的两点必定位于原点两侧
   • 原点就是这两点连线的中点
   • 例如：点A和点B表示的数互为相反数，那么原点就在AB的正中间

3. 绝对值问题：要找出绝对值最大的数，只需要看哪个点离原点最远。

数轴应用实例解析

1. 实际问题分析：

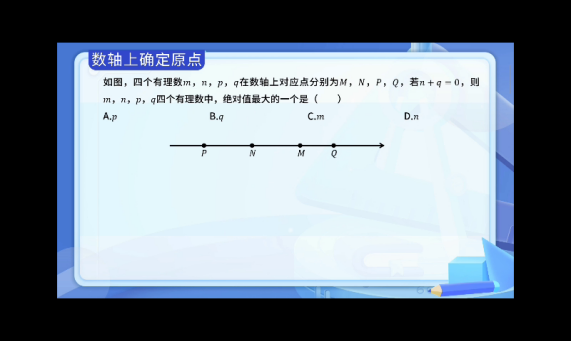
   • 将N、P、Q、R四个有理数标注在数轴上
   • 已知N+Q=0，说明N和Q互为相反数
   • 因此原点必定在N和Q的正中间

2. 绝对值判断：

   • 标出原点位置后
   • 观察各点与原点的距离
   • 离原点最远的点P对应的数绝对值最大

3. 关键知识点：互为相反数的两个数在数轴上到原点的距离相等。

数轴单位长度的确定

1. 单位长度计算：

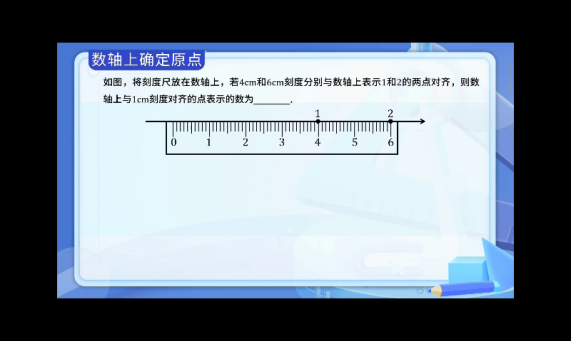
   • 已知4厘米对应数轴上的1
   • 6厘米对应数轴上的2
   • 所以2个单位长度=6-4=2厘米
   • 因此1个单位长度=1厘米

2. 原点定位：

   • 从初始位置向左移动2厘米找到原点
   • 原点位于刻度尺的2厘米处

3. 数值确定：

   • 1厘米刻度对应的点到原点距离为1厘米
   • 即0.5个单位长度
   • 因为该点在原点左侧，所以表示的数是-0.5

原点位置的多种可能性

1. 排除法分析：

   • 原点不可能在点N或点P
   • 因为这与条件|A|+|B|=3矛盾

2. 可能位置验证：

   • 当原点在点M时：
     • 数A对应的点到M的距离
     • 数B对应的点到R的距离
     • 满足|A|+|B|=3
   • 当原点在点R时同样满足条件

3. 结论：原点可能的位置是点M或点R，对应选项B。