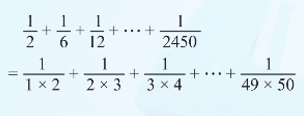初中数学营地：有理数简算之列差法

嗨，同学们好！欢迎来到初中数学营地。今天我们要学习有理数简算中的一种新方法——列差法。

什么是列差法？

让我们先看一个简单的例子：

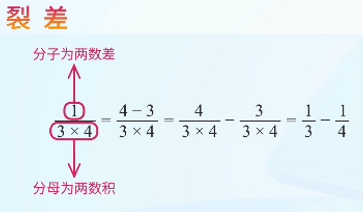
3×4 分之 1

这里分母是3×4，分子是1。注意到4和3的差正好是1，我们可以这样拆分：

3×4 分之 1 = 3×4 分之 (4-3) = 3×4 分之 4 - 3×4 分之 3 = 1/3 - 1/4

这样就成功地将一个分数拆成了两个分数之差。

列差法的适用条件：

• 分母为两个数的乘积
• 分子正好是这两个数的差

列差法的实际应用

看起来这个方法很简单，但它有什么用呢？让我们看一个实际例子：

计算：

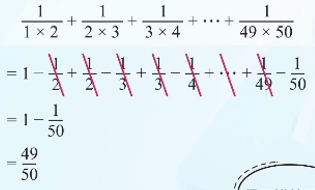
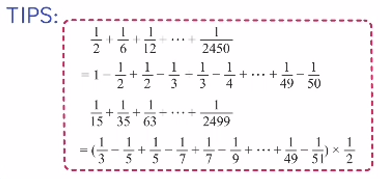
1×2 分之 1 + 2×3 分之 1 + 3×4 分之 1 + ... + 49×50 分之 1

按照列差法，我们可以这样拆分每一项：

• 第一项：1×2 分之 1 = 1 - 1/2
• 第二项：2×3 分之 1 = 1/2 - 1/3
• 第三项：3×4 分之 1 = 1/3 - 1/4
• ...
• 最后一项：49×50 分之 1 = 1/49 - 1/50

把这些拆分后的式子相加，会发现中间的项都互相抵消了，最后只剩下：

1 - 1/50 = 49/50

是不是很神奇？这就是列差法的威力！

更复杂的情况

情况一：分母不是直接的两数相乘

如果题目是这样的：

我们可以看到又回到了之前的题型

情况二：分子不为1

列差法不仅适用于分子为1的情况，比如：

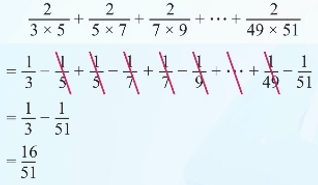
3×5 分之 2 + 5×7 分之 2 + 7×9 分之 2 + ... + 49×51 分之 2

可以这样拆分：

• 3×5 分之 2 = 1/3 - 1/5
• 5×7 分之 2 = 1/5 - 1/7
• 7×9 分之 2 = 1/7 - 1/9
• ...
• 49×51 分之 2 = 1/49 - 1/51

相加后结果为：

1/3 - 1/51 = 16/51

情况三：另外一种类型

关键要点总结

1. 适用条件：分母为两数乘积，分子是这两数的差（可以是一，也可以是其他数）
2. 拆分方法：将分数拆分为两个分数的差
3. 简化计算：通过拆分后的相互抵消，大大简化求和过程
4. 调整技巧：当分子不是两数差时，可以通过乘以适当的系数来调整

练习建议

为了熟练掌握列差法，建议同学们多练习以下几类题目：

1. 简单的列差拆分（如1/(n×(n+1))）
2. 分母间隔更大的情况（如1/(n×(n+2))）
3. 分子不为1的情况
4. 综合性的多个分数相加
   
   今天的课程就到这里，希望同学们能够掌握这个强大的简算工具。下次课我们将学习更多有趣的数学技巧，再见！