初中数学营地：有理数的异号加法详解

同学们好！欢迎来到初中数学营地。今天我们要学习的是有理数的异号加法。在前面的课程中，我们已经掌握了同号有理数相加的计算方法，那么当遇到符号不同的两个数相加时，该如何计算呢？让我们一起来探索这个有趣的问题！

一、特殊情况：互为相反数的加法

首先，我们来回顾一个特殊情况：如果两个数互为相反数，比如3和-3，或者-5和5，它们的和是多少呢？

根据相反数的定义：

• 3 + (-3) = 0
• (-5) + 5 = 0

结论：互为相反数的两个数相加，结果为零。

二、一般情况：不互为相反数的异号加法

当两个异号数不互为相反数时，该怎么计算呢？让我们通过一个生活中的例子来理解。

实例分析

情景描述：
小红从家门口出发：

1. 先向西走3米
2. 然后掉头向东走5米
   最后她在什么位置？

设定：

• 以家门口为原点（0点）
• 向东为正方向，记作"+"
• 向西为负方向，记作"-"

数轴表示：

<---|----|----|----|----|----|--->
   -3   -2   -1    0    1    2

计算过程：

• 向西走3米：-3
• 向东走5米：+5
• 总位移：(-3) + 5 = ?

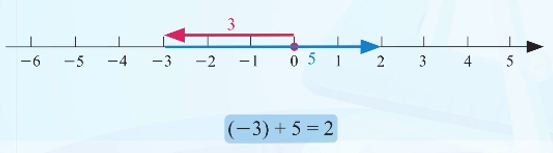
观察数轴可以发现，小红最终位于原点右侧2米处，因此：
(-3) + 5 = 2

另一个例子

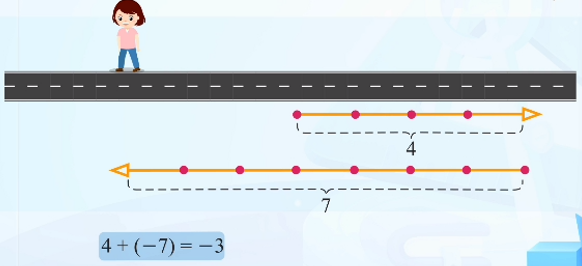
如果小红先向东走4米，再向西走7米：

• 向东走4米：+4
• 向西走7米：-7
• 总位移：4 + (-7) = ?

最终位置在原点左侧3米处：
4 + (-7) = -3

三、异号加法的通用法则

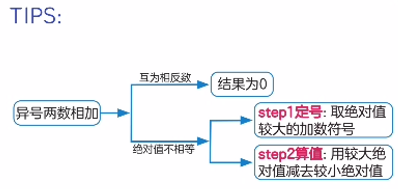
通过上面的例子，我们可以总结出异号加法的计算步骤：

1. 比较绝对值大小：找出两个数中绝对值较大的数
2. 确定和的符号：和的符号与绝对值较大的数相同
3. 计算数值部分：用较大的绝对值减去较小的绝对值

口诀：异号相加看大小，符号跟着大的跑，数值相减错不了

示例计算

计算 3784 + (-5768)：

1. 比较绝对值：

   • |3784| = 3784
   • |-5768| = 5768
   • 5768 > 3784

2. 确定符号：

   • 5768是负数，所以结果符号为负

3. 计算数值：

   • 5768 - 3784 = 1984

因此：3784 + (-5768) = -1984

四、计算步骤总结

进行异号加法运算时，按照以下步骤进行：

1. 判断是否为相反数：

   • 如果是，结果直接为0
   • 如果不是，继续下一步

2. 确定符号：

   • 比较两数的绝对值
   • 和的符号与绝对值较大的数相同

3. 计算数值：

   • 用较大的绝对值减去较小的绝对值

五、课堂练习

试着计算以下题目：

1. (-12) + 7 = ?
2. 15 + (-20) = ?
3. (-3.5) + 2.8 = ?
4. 1/2 + (-3/4) = ?

（答案将在下节课揭晓）

六、总结

今天我们学习了有理数的异号加法，关键要记住：

• 互为相反数的两数相加得0
• 不互为相反数时，要比较绝对值大小
• 和的符号与绝对值较大的数相同
• 数值部分用大绝对值减小绝对值
  
  希望同学们能够熟练掌握这个方法。下次课我们将学习有理数加法的综合应用，敬请期待！