有理数加减的实际应用

我们通过两个具体的例子来学习和理解今天的知识点

工厂每日生产情况

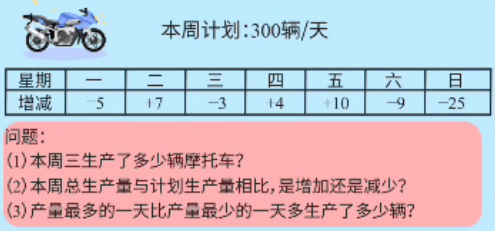
• 本周计划：每日生产300辆摩托车
• 实际生产量与计划量的差异表示方法：
  • 负数表示低于计划量（如"-5"表示少生产5辆）
  • 正数表示超过计划量（如"+7"表示多生产7辆）
    
    示例说明
    周三实际生产情况：
• 计划量：300辆
• 差额：-3辆（比计划少生产3辆）
• 实际产量：300 + (-3) = 297辆

周生产总结

1. 总生产量分析：

   • 通过求每日增减量的和得出总差异
   • 本周求和结果：-21
   • 结论：总产量比计划少21辆

2. 单日产量波动：

   • 产量最多与最少日的差额：35辆
   • 计算方法：最大增减值 - 最小增减值

小虫爬行实验分析

运动轨迹

• 方向约定：
  • 向右：正数
  • 向左：负数
• 通过记录每次爬行距离确定路径和最终位置
  

  实验结果

  1. 最终位置：
     • 位移总和为0
     • 结论：回到出发点O

2. 最远距离：

   • 最大偏离距离：12cm
   • 计算方法：爬行过程中与O点的最大距离

3. 奖励机制：

   • 每爬行2cm奖励1粒芝麻
   • 总爬行距离：54cm
   • 获得芝麻数：54 ÷ 2 = 27粒

问题解决要点

1. 核心关注：

   • 总运动距离（与方向无关）
   • 每次运动后的即时位置

2. 计算方法：

   • 方向用正负表示
   • 通过累加计算实时位置
   • 比较得出最大偏离值