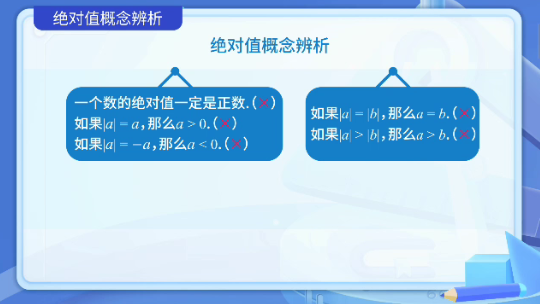
12、绝对值概念辨析
初中数学绝对值概念深度解析:通过四道关卡挑战,全面掌握绝对值的正负性、逆命题、相反数关系和大小比较。重点解析常见误区,强调0的特殊性、数轴思维和分类讨论方法,帮助理解"绝对值等于本身是非负数"、"|A|=-A时A≤0"等核心结论,提升绝对值问题的解题能力。
初中数学绝对值概念深度解析
同学们好!欢迎来到初中数学营地。今天我们要一起攻克绝对值这个重要概念。在前面的学习中,我们已经知道:
- 数轴上表示数A的点与原点的距离叫做A的绝对值,记作|A|
- 例如:|3|=3,|-2|=2,|0|=0
- 正数的绝对值是它本身
- 负数的绝对值是它的相反数
- 零的绝对值是零
但想要完全掌握这个概念,我们还需要通过四道关卡来检验理解程度。准备好了吗?开始挑战!
第一关:绝对值的正负性
命题:一个数的绝对值一定是正数吗?
让我们仔细分析:
- 正数的绝对值确实是正数(如|5|=5)
- 负数的绝对值也是正数(如|-3|=3)
- 但是0呢?|0|=0,而0既不是正数也不是负数
结论:原说法错误。正确的说法应该是"一个数的绝对值一定是非负数"。
第二关:绝对值的逆命题
命题:绝对值等于它本身的数一定是正数。
这个命题看起来像是第一关结论的逆命题。但数学中,原命题正确并不意味着逆命题也正确。
举例说明:
- "苹果是水果"正确
- 但"水果是苹果"就明显错误
回到绝对值:
- 正数的绝对值等于它本身(如|7|=7)
- 但0的绝对值也等于它本身(|0|=0)
结论:原说法错误。正确的应该是"绝对值等于它本身的数是非负数(即≥0)"。
第三关:绝对值与相反数
命题:如果|A|=-A,那么A<0。
分析:
- 当A>0时:|A|=A ≠ -A
- 当A=0时:|0|=0=-0
- 当A<0时:|A|=-A(如|-5|=5=-(-5))
结论:原说法不完全正确。更准确的说法是"A≤0"。
第四关:绝对值相等的数
命题:如果|A|=|B|,那么A=B。
让我们用数轴来理解:
- 两个数到原点的距离相等,可能有几种情况:
- A=B(如|3|=|3|)
- A=-B(如|4|=|-4|)
结论:原说法不全面。正确的结论是"A=B或A=-B",可以简写为"A=±B"。
终极挑战:绝对值大小比较
命题:如果|A|>|B|,那么A>B。
还是用数轴分析:
- 都在右侧:A=3,B=2 → 3>2(成立)
- 都在左侧:A=-3,B=-2 → -3<-2(不成立)
- 一正一负:A=3,B=-2 → 3>-2(成立)
- 其他组合...
结论:原说法不完全正确。|A|>|B|只能说明A离原点更远,不能直接比较A和B的大小。
总结要点
- 0的特殊性:讨论正负数时,永远不要忘记0这个特例
- 逆命题:原命题正确≠逆命题正确
- 数轴思维:遇到绝对值问题,画数轴辅助理解
- 分类讨论:正数、负数、零三种情况要全面考虑
通过这四关的挑战,相信大家对绝对值的理解更加深入了。记住这些要点,绝对值问题就能迎刃而解啦!我们下期再见~
收藏