初中数学营地：绝对值与原数的奥秘探索

同学们好！欢迎来到初中数学营地！今天我们要一起攻克"根据绝对值求原数"这个重要知识点。上节课我们已经顺利通过四道关卡，将辨析绝对值的技能成功提升到了满级。但绝对值这个概念可不会这么容易就被我们降服哦！你看，它正带着三个"兄弟"在数字城堡里兴风作浪呢，让我们一起来会会它们！

第一关：绝对值的本质理解

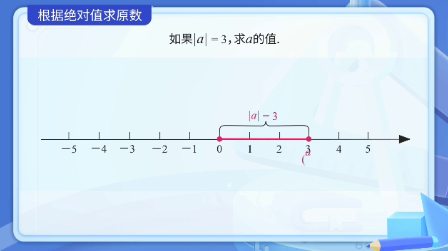
例题1：如果|A|=3，求A的值。

这个题目其实很简单。我们知道，绝对值表示的是数轴上点到原点的距离，也就是图中这段线段的长度。那么题目可以理解为：如果一个点到原点的距离为3，那么这个点可能在什么位置呢？

• 在原点右侧3个单位长度处，这时A=3
• 在原点左侧3个单位长度处，这时A=-3

综合这两种情况，答案应该是3或-3。我们也可以总结出一个重要结论：

结论1：如果|A|=b（b为正数），那么A=b或A=-b，也可以简写为A=±b。

第二关：绝对值不等式的应用

例题2：绝对值小于4的整数有几个？

我们还是请出数轴将军来帮忙。首先，绝对值等于4的数是4和-4。题目要求绝对值小于4，那么在-4和4之间的所有整数都符合条件。

具体来看有：

• 负数部分：-3、-2、-1
• 零：0
• 正数部分：1、2、3

总共有7个整数符合要求。

我们也可以用另一种思路理解：
要找绝对值小于4的整数，其实就是找出绝对值为0、1、2、3的数：

• |A|=3 → A=±3
• |A|=2 → A=±2
• |A|=1 → A=±1
• |A|=0 → A=0

这样同样得到7个数的结果。

第三关：多重绝对值的综合应用

例题3：已知|A|=2，|B|=5，且B<A，求A、B的值。

根据绝对值的性质，我们可以得出：

• A的可能值：2或-2
• B的可能值：5或-5

组合起来有四种情况：

1. A=2，B=5
2. A=2，B=-5
3. A=-2，B=5
4. A=-2，B=-5

但题目还附加了一个条件：B<A。让我们逐一验证：

1. A=2，B=5 → 5<2？不成立
2. A=2，B=-5 → -5<2？成立
3. A=-2，B=5 → 5<-2？不成立
4. A=-2，B=-5 → -5<-2？成立

因此，符合条件的组合有两种：

• A=2，B=-5
• A=-2，B=-5

知识总结

通过今天的三个关卡，我们不仅打败了绝对值的三个"兄弟"，还总结出了解决这类问题的关键结论：

1. 单一绝对值方程：|A|=b（b≥0）的解为：

   • 当b>0时，A=±b
   • 当b=0时，A=0

2. 绝对值不等式：|A|<b（b>0）的解为-b<A<b

3. 多重绝对值问题的解题步骤：

   • 分别求出每个绝对值的可能值
   • 列出所有可能的组合
   • 根据附加条件筛选有效解
     
     记住这些结论，下次遇到绝对值问题就能轻松应对啦！今天的数学冒险就到这里，我们下次再见！