初中数学营地：绝对值的非负性详解

同学们好！欢迎来到初中数学营地。今天我们要一起学习绝对值的非负性这个重要知识点。

一、回顾绝对值的基本概念

在前面的学习中，我们已经对绝对值很熟悉了。比如：

• 计算具体数的绝对值：|3|=3，|-3|=3
• 化简含有绝对值的式子

现在思考一个问题：哪个数的绝对值是-3呢？

让我们一起来分析：

• 3的绝对值是3
• -3的绝对值也是3
• 0的绝对值是0

通过思考可以发现：任何数的绝对值都不可能是负数！这就是我们要学习的绝对值的非负性。

二、绝对值的非负性详解

绝对值的非负性是指：

1. 正数的绝对值是它本身（还是正数）
2. 负数的绝对值是它的相反数（变成正数）
3. 0的绝对值是0（非负数）

结论：任何实数的绝对值都是非负数（即≥0）。

三、实战应用

例题1

已知 |A - 1| + |B + 2| = 0，求A和B的值。

分析过程：

1. 两个绝对值相加等于0
2. 绝对值都是非负的（≥0）
3. 要使和为0，必须每个绝对值都为0

解题步骤：

1. |A - 1| = 0 ⇒ A - 1 = 0 ⇒ A = 1
2. |B + 2| = 0 ⇒ B + 2 = 0 ⇒ B = -2

例题2（难度提升）

已知 |A - 1| + |B + 2| + |C - 3| = 0，求A、B、C的值。

分析过程：
虽然式子变复杂了，但原理相同：

1. 三个绝对值相加等于0
2. 每个绝对值都是非负的
3. 和为零 ⇒ 每个绝对值都必须为零

解题步骤：

1. |A - 1| = 0 ⇒ A = 1
2. |B + 2| = 0 ⇒ B = -2
3. |C - 3| = 0 ⇒ C = 3

四、规律总结

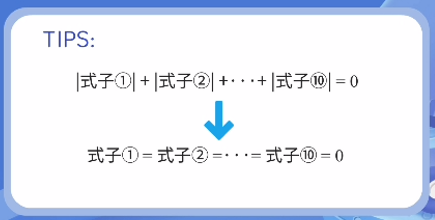
对于这类绝对值相加等于0的问题，无论有多少个绝对值相加，都有以下规律：

1. 每个绝对值都必须为0
2. 绝对值符号内的表达式等于0
3. 解这些方程就能求出未知数的值

记忆口诀：

绝对值和非负性，
相加为零要记清。
每个绝对值为零时，
解出答案真容易！

五、课后思考

请同学们思考：

1. 如果改为 |A| + |B| = 1，A和B有多少种可能？
2. |x - 2| 的最小值是多少？此时x等于多少？

今天的课程就到这里，希望大家掌握了绝对值的非负性。下次课我们将学习绝对值的其他应用，再见！