初中数学营地：绝对值的几何意义详解

一、绝对值的基本概念

同学们好！欢迎来到初中数学营地。今天我们要一起探索绝对值的几何意义这个有趣的知识点。

在前面的课程中，我们已经知道：

• 一个数A的绝对值（记作|A|）表示数轴上表示A的点到原点的距离
• 例如：|3| = 3，表示3到0的距离是3；|-2| = 2，表示-2到0的距离是2

二、绝对值表达式的几何意义

1. |x - a| 的几何意义

|x - a|表示的是点x到点a的距离。例如：

• |x - 2|表示点x到2的距离
• |x + 1|可以转化为|x - (-1)|，表示点x到-1的距离

2. 多个绝对值相加的意义

当我们遇到多个绝对值相加时，比如|x - a| + |x - b|，它表示的是点x到点a和点b的距离之和。

三、绝对值求和的最小值问题

情况1：两个绝对值相加

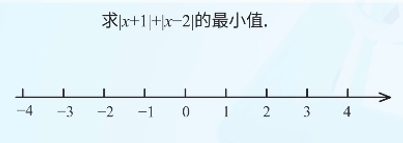
例题1：求|x + 1| + |x - 2|的最小值

解题步骤：

1. 在数轴上标出-1和2两个点
2. 分析x在不同位置时的距离和：
   • 当x < -1时：距离和 = (-1 - x) + (2 - x) = 3 - 2x > 3
   • 当-1 ≤ x ≤ 2时：距离和 = (x + 1) + (2 - x) = 3
   • 当x > 2时：距离和 = (x + 1) + (x - 2) = 2x - 1 > 3

结论：当x在-1和2之间时，|x + 1| + |x - 2|取得最小值3。

情况2：四个绝对值相加（偶数个）

例题2：求|x + 1| + |x - 2| + |x - 3| + |x - 4|的最小值

解题方法：

1. 将绝对值分成两组：
   • 第一组：|x + 1| + |x - 4|（最小值5，当-1 ≤ x ≤ 4时）
   • 第二组：|x - 2| + |x - 3|（最小值1，当2 ≤ x ≤ 3时）
2. 要同时满足两组都取最小值，x必须在2和3之间

结论：当2 ≤ x ≤ 3时，整个表达式取得最小值6（5+1）。

情况3：三个绝对值相加（奇数个）

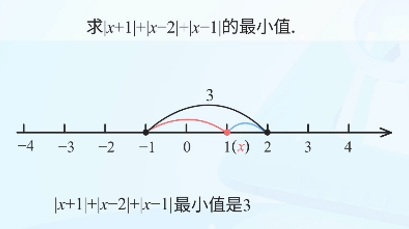
例题3：求|x + 1| + |x - 1| + |x - 2|的最小值

解题步骤：

1. 先看|x + 1| + |x - 2|（最小值3，当-1 ≤ x ≤ 2时）
2. 再加上|x - 1|，为了使总和最小，x应该等于1
3. 此时|x - 1| = 0，总和为3 + 0 = 3

结论：当x=1时，表达式取得最小值3。

情况4：五个绝对值相加（奇数个）

例题4：求|x + 1| + |x - 1| + |x - 2| + |x - 3| + |x - 4|的最小值

解题方法：

1. 将绝对值分成两组：
   • 第一组：|x + 1| + |x - 4|（最小值5，当-1 ≤ x ≤ 4时）
   • 第二组：|x - 1| + |x - 2| + |x - 3|
2. 对于第二组，当x=2时取得最小值2
3. 因此当x=2时，整个表达式取得最小值7（5+2）

四、规律总结

通过以上例题，我们可以总结出以下规律：

1. 偶数个绝对值相加：

   • 最小值出现在中间两个数之间的区间
   • 例如：|x - a| + |x - b| + |x - c| + |x - d|（假设a < b < c < d）
   • 最小值出现在b ≤ x ≤ c时

2. 奇数个绝对值相加：

   • 最小值出现在中间那个数对应的点
   • 例如：|x - a| + |x - b| + |x - c|（假设a < b < c）
   • 最小值出现在x=b时

五、课后练习

1. 求|x - 1| + |x - 3|的最小值及x的范围
2. 求|x + 2| + |x - 1| + |x - 4|的最小值及x的值
3. 求|x - 1| + |x - 2| + |x - 3| + |x - 4|的最小值及x的范围

同学们，今天的课程就到这里。记住要多多练习，才能真正掌握这个知识点哦！我们下次再见！